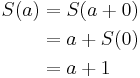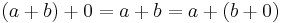Proofs involving the addition of natural numbers

Mathematical proofs for addition of the natural numbers: additive identity, commutativity, and associativity. These proofs are used in the article Addition of natural numbers.

Contents

Definitions

This article will use the definitions in addition of natural numbers, particularly [A1] and [A2]:

For the proof of commutativity, it is useful to define another natural number closely related to the successor function, namely "1". We define 1 to be the successor of 0, in other words,

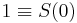1 \equiv S(0)\,.

Note that for all natural numbers a,

\begin{align} S(a) &= S(a %2B 0)\\ &= a %2B S(0)\\ &= a %2B 1 \end{align}

due to [A1] and [A2].

Proof of associativity

We prove associativity by first fixing natural numbers a and b and applying induction on the natural number c.

For the base case c = 0,

(a%2Bb)%2B0=a%2Bb=a%2B(b%2B0)

Each equation follows by definition [A1]; the first with a + b, the second with b.

Now, for the induction. We assume the induction hypothesis, namely we assume that for some natural number c,

(a%2Bb)%2Bc=a%2B(b%2Bc)

Then it follows,

(a + b) + S(c)
= S((a + b) + c) [by A2]
= S(a + (b + c)) [by the induction hypothesis]
= a + S(b + c) [by A2]
= a + (b + S(c)) [by A2]

In other words, the induction hypothesis holds for S(c). Therefore, the induction on c is complete.

Proof of identity element

Definition [A1] states directly that 0 is a right identity. We prove that 0 is a left identity by induction on the natural number a.

For the base case a = 0, 0 + 0 = 0 by definition [A1]. Now we assume the induction hypothesis, that 0 + a = a. Then

0 + S(a)
= S(0 + a) [by A2]
= S(a) [by the induction hypothesis]

This completes the induction on a.

Proof of commutativity

We prove commutativity (a + b = b + a) by applying induction on the natural number b. First we prove the base cases b = 0 and b = S(0) = 1 (i.e. we prove that 0 and 1 commute with everything).

The base case b = 0 follows immediately from the identity element property (0 is an additive identity), which has been proved above: a + 0 = a = 0 + a.

Next we will prove the base case b = 1, that 1 commutes with everything, i.e. for all natural numbers a, we have a + 1 = 1 + a. We will prove this by induction on a (an induction proof within an induction proof). Clearly, for a = 0, we have 0 + 1 = 0 + S(0) = S(0 + 0) = S(0) = 1 = 1 + 0. Now, suppose a + 1 = 1 + a. Then

S(a) + 1
= S(a) + S(0)
= S(S(a) + 0) [by A2]
= S((a + 1) + 0)
= S(a + 1) [by A1]
= S(1 + a) [by the induction hypothesis]
= 1 + S(a) [by A2]

This completes the induction on a, and so we have proved the base case b = 1. Now, suppose that for all natural numbers a, we have a + b = b + a. We must show that for all natural numbers a, we have a + S(b) = S(b) + a. We have

a + S(b)
= a + (b + 1)
= (a + b) + 1 [by associativity]
= (b + a) + 1 [by the induction hypothesis]
= b + (a + 1) [by associativity]
= b + (1 + a) [by the base case b = 1]
= (b + 1) + a [by associativity]
= S(b) + a

This completes the induction on b.

See also

References